几种排序算法 | lyq1996的博客

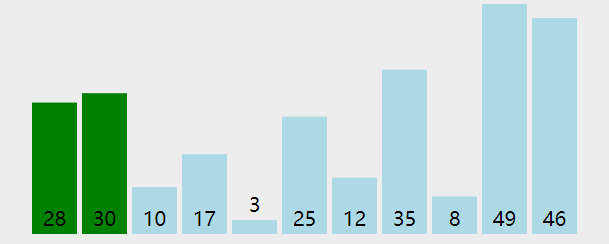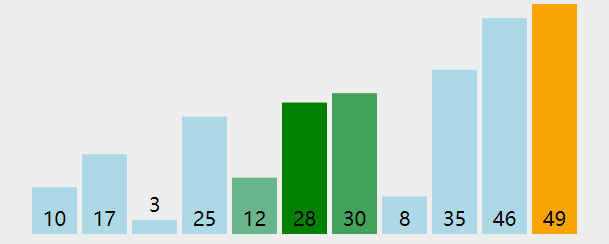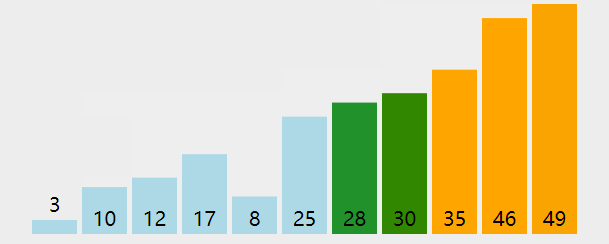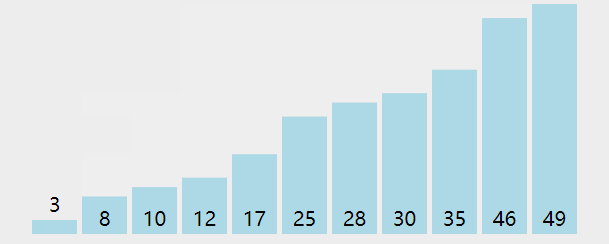
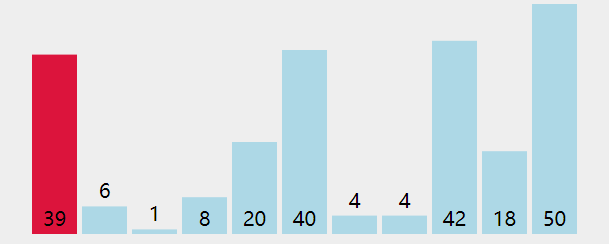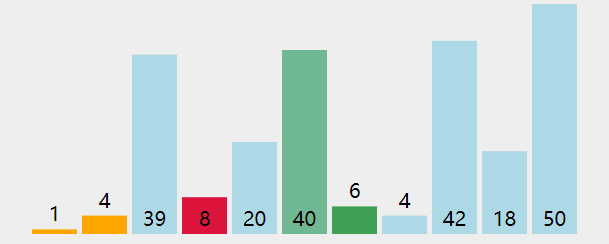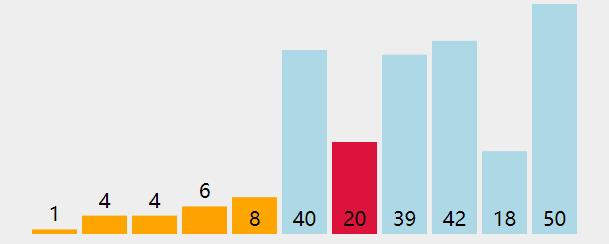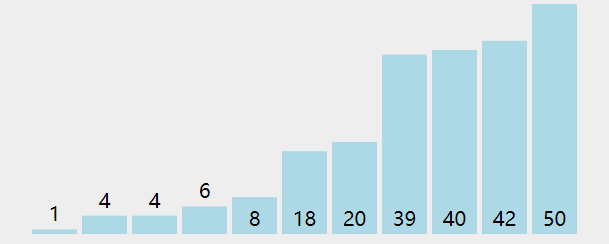
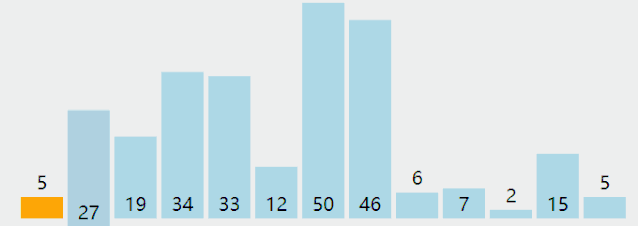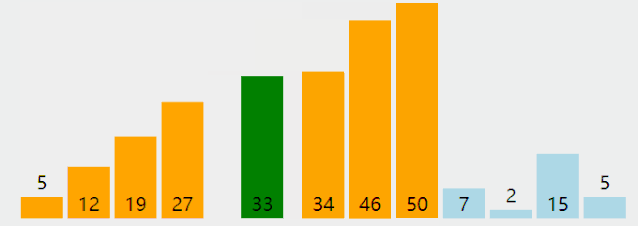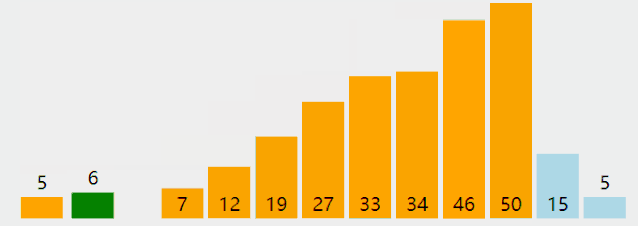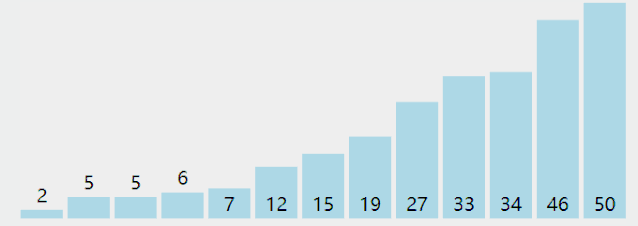
排序算法

1 冒泡(Bubble Sort)

图解

空间复杂度 1
平均时间复杂度 n^2
最坏时间复杂度 n^2
最好时间复杂度 n
稳定性 Y

算法步骤

相邻的元素。如果第一个比第二个大，就交换他们两个；
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数；
针对所有的元素重复以上的步骤，除了最后一个；
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

code

static int *bubbleSort(int input[])
{
    static int ret[200];
    int temp;
    memcpy(ret, input, sizeof(int) * 200);
    for (int i = 0; i < 199; i++)
    {
        for (int j = 0; j < 199 - i; j++)
        {
            if (ret[j] > ret[j + 1])
            {
                temp = ret[j];
                ret[j] = ret[j + 1];
                ret[j + 1] = temp;
            }
        }
    }
    return ret;
}

2 选择(Selection Sort)

图解

空间复杂度 1
平均时间复杂度 n^2
最坏时间复杂度 n^2
最好时间复杂度 n^2
稳定性 N

算法步骤

在未排序序列中找到最小（大）元素，存放到排序序列的起始位置；
然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾；
以此类推，直到所有元素均排序完毕。

code

static int *selectSort(int input[])
{
    static int ret[200];
    int temp;
    int min;
    memcpy(ret, input, sizeof(int) * 200);
    for (int i = 0; i < 200; i++)
    {
        min = i;
        for (int j = i; j < 200; j++)
        {
            if (ret[j] < ret[min])
            {
                min = j; //mark the min.
            }
        }
        temp = ret[i]; //exchange ret[min] and ret[i]
        ret[i] = ret[min];
        ret[min] = temp;
    }
    return ret;
}

3 插入排序(Insertion Sort)

图解

空间复杂度 1
平均时间复杂度 n^2
最坏时间复杂度 n^2
最好时间复杂度 n
稳定性 Y

算法步骤

从第一个元素开始，该元素可以认为已经被排序；
取出下一个元素，在已经排序的元素序列中从后向前扫描；
如果该元素（已排序）大于新元素，将该元素移到下一位置；
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
将新元素插入到该位置后；
重复步骤2~5。

code

static int *insertSort(int input[])
{
    static int ret[200];
    int temp;
    int j;
    memcpy(ret, input, sizeof(int) * 200);
    for (int i = 0; i < 199; i++)
    {
        temp = ret[i + 1];
        for (j = i + 1; j > 0; j--)
        {
            if (ret[j - 1] > temp)
            {
                ret[j ] = ret[j - 1];
            }
            else
            {
                break;
            }
        }
        ret[j] = temp;
    }
    return ret;
}

4 希尔排序(Shell Sort)

空间复杂度 1
平均时间复杂度 n^1.3
最坏时间复杂度 n^2
最好时间复杂度 n
稳定性 N

思想:将数列依据增量序列Dk分割成若干个子序列，对每个Dk应用”Dk间隔”直接插入排序，最后再来一次排序。
例增量序列：

1	{1,3,7,15}

Dk取值如(2^n)-1:
1、3、7、15、31….

static void shell_sort(int index, int vaaa[]) {
  int power = log2(index);       //比如输入16个数,那么power=4
  int temp;
  int j;
  while (power) {
    int dk = pow(2, power) - 1;  //一趟增量为dk=2^power - 1 的插入排序, 依次为 15 7 3 1
    printf("increment:%d\n", dk);
    for (int x = 0; x < dk; x++) {  //将需要排序的数组按0-dk分割
      printf("x: %d\n", x);
      //把插入排序的i++改成i+=dk,0改为x,i<index改为i + dk < index
      for (int i = x; i + dk < index; i += dk) {  //以插入排序x,x+dk,x+dk+dk....排序, 0<=x<dk,
        printf("Enter sub insection sort.\n");
        temp = vaaa[i + dk];
        for (j = i + dk; j > 0; j -= dk) {
          if (temp < vaaa[j - dk] && j - dk >= 0) { //防止数组越界
            vaaa[j] = vaaa[j - dk]; //后一个等于前一个,为temp腾位置
          } else {
            break;
          }
        }
        vaaa[j] = temp; //插入temp
      }
    }
    printf("increment: %d and result:", dk);
    for (int i = 0; i < index; i++) {
      printf("%d ", vaaa[i]);
    }
    std::cout << std::endl;
    power--;
  }
}

5 堆排序(Heap Sort)

空间复杂度 1
平均时间复杂度 nLog2n
最坏时间复杂度 nLog2n
最好时间复杂度 nLog2n
稳定性 N

父节点 > 子节点变成一个堆
完全二叉树

对于一个完全二叉树，如何变成一个堆？从倒数第二个节点开始，与它的子节点比较，拿出最大的放在父节点上。
变成一个堆后，拿出根节点(根节点最大)，再对跟节点作”堆”化

6. 归并排序(Merge Sort)

空间复杂度 n
平均时间复杂度 nLog2n
最坏时间复杂度 nLog2n
最好时间复杂度 nLog2n
稳定性 Y

将序列a分割成两个已经排序的元素序列b、c，取3个指针，分别指向a，b，和c
当a不是最后一个元素，比较b和c的大小，若b小于c，a=b，a++，b++，反之a=c，a++，c++

所以就是递归，不断将元素分割，直到分割后只有一个元素了退出递归。

和leetcode上面一题：求给定一个排序好的数组，求某一个元素给定范围的数组一样。

#include <iostream>

void merge(int L, int R, int mid, int var[]) {
  int tmp1[mid - L];
  int tmp2[R - mid + 1];
  int i, j, o;
  for (i = L; i < mid; i++) {
    tmp1[i - L] = var[i];
  }
  for (j = mid; j <= R; j++) {
    tmp2[j - mid] = var[j];
  }
  i = 0;
  j = 0;
  o = L;
  while (i < mid - L && j < R - mid + 1) {
    if (tmp1[i] < tmp2[j]) {
      var[o++] = tmp1[i++];
    } else {
      var[o++] = tmp2[j++];
    }
  }
  // 一个结束了,也许另一个还未
  while (i < mid - L) {
    var[o++] = tmp1[i++];
  }
  while (j < R - mid + 1) {
    var[o++] = tmp2[j++];
  }
}

void mergeSort(int L, int R, int var[]) {
  if (L == R) {
    return;
  }
  int mid = (L + R) / 2;
  mergeSort(L, mid, var);
  mergeSort(mid + 1, R, var);
  merge(L, R, mid + 1, var);
}

int main() {
  using std::cin;
  using std::cout;
  using std::endl;

  int var[1000] = {0};
  int buff = 0;
  int index = 0;
  int count = 0;

  while (cin >> buff) {
    var[index] = buff;
    index++;
    if (getchar() == '\n') {
      break;
    }
  }
  mergeSort(0, index - 1, var);
  for (int i = 0; i < index; i++) {
    printf("%d ", var[i]);
  }
}

7. 快排(Quick Sort)

空间复杂度 nLog2n
平均时间复杂度 nLog2n
最坏时间复杂度 n^2
最好时间复杂度 nLog2n
稳定性 N

8. 桶排序(Bucket Sort)

空间复杂度 n+k
平均时间复杂度 n+k
最坏时间复杂度 n^2
最好时间复杂度 n
稳定性 Y

9. 计数排序(Counting Sort)

空间复杂度 n+k
平均时间复杂度 n+k
最坏时间复杂度 n+k
最好时间复杂度 n+k
稳定性 Y

10. 基数排序(Radix Sort)

空间复杂度 n+k
平均时间复杂度 nk
最坏时间复杂度 nk
最好时间复杂度 n*k
稳定性 Y

未完待续