DFS和BFS简单总结 | lyq1996的博客

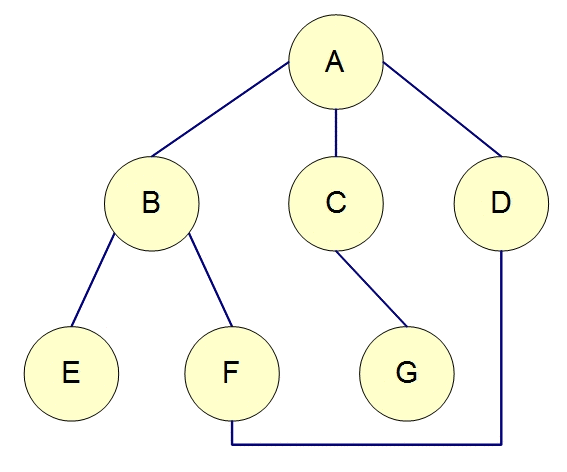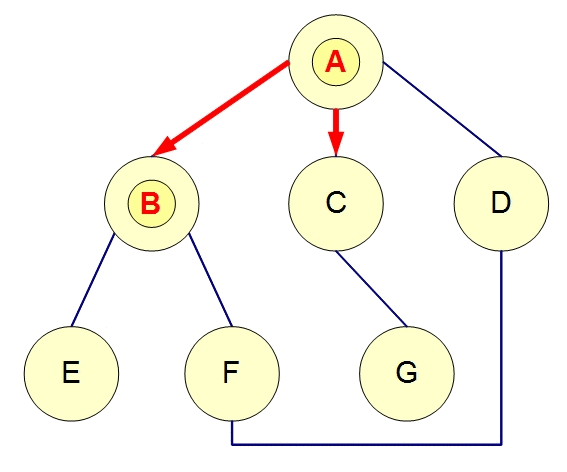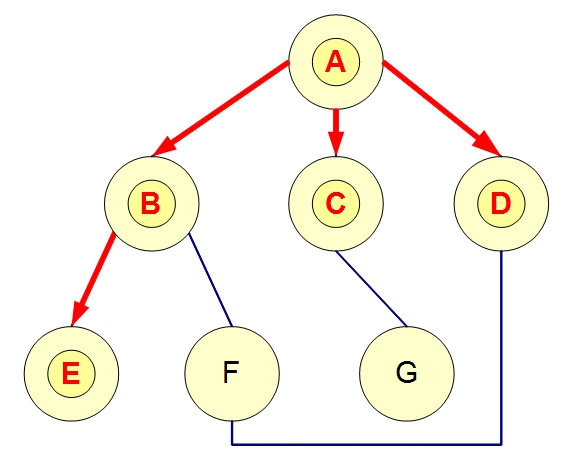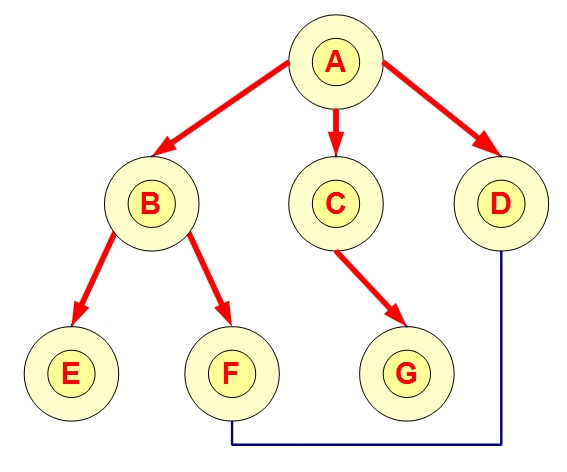
总结

这两个是图的基本算法，很简单。

转载一下别人的总结
版权声明：本文为CSDN博主「EbowTang」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/EbowTang/article/details/44263635

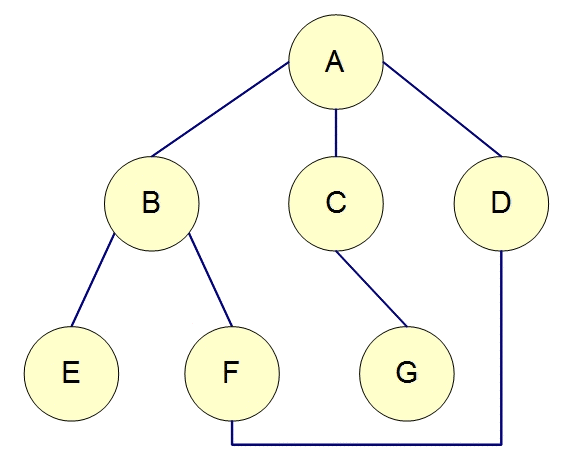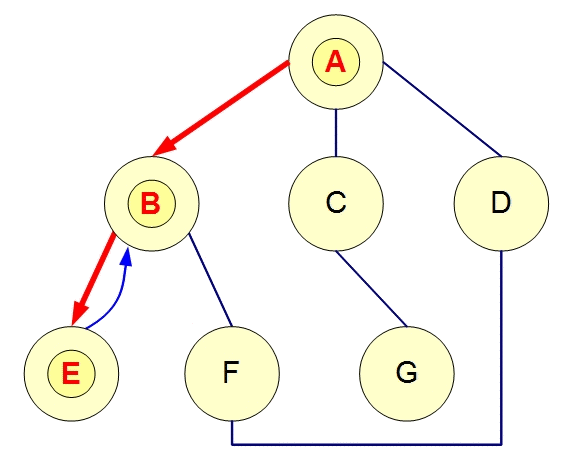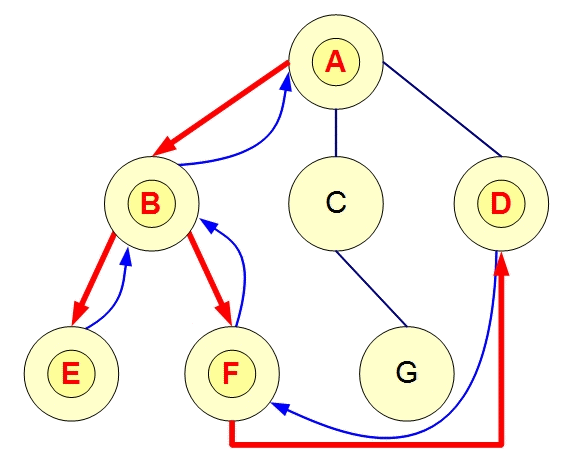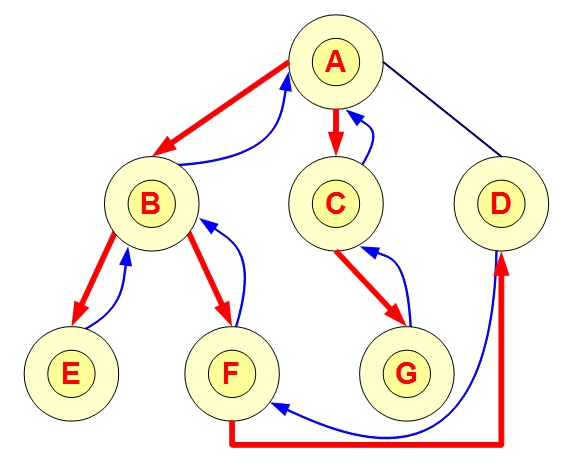
DFS的思想是一条路走到底，走不到底就回到上个状态点。

如果可能，访问一个邻接的未访问顶点，标记它，并把它放入栈中。
当不能执行规则1时，如果栈不空，就从栈中弹出一个顶点。（返回上一个顶点）
如果不能执行规则1和规则2，就完成了整个搜索过程。

伪代码：

{
	mark v as visited //标记顶点为已访问  
	for each w adjacent to v //将邻顶点变成新的当前顶点  
	{
		if w unvisited//若这个新的当前节点没有被访问过  
		{
			dfs(w) //递归调用  
		}
	}
}

广度优先搜索较之深度优先搜索之不同在于，深度优先搜索旨在不管有多少条岔路，先一条路走到底，不成功就返回上一个路口然后就选择下一条岔路，而广度优先搜索旨在面临一个路口时，把所有的岔路口都记下来，然后选择其中一个进入，然后将它的分路情况记录下来，然后再返回来进入另外一个岔路，并重复这样的操作。

访问下一个未来访问的邻接点，这个顶点必须是当前顶点的邻接点，标记它，并把它插入到队列中。
如果因为已经没有未访问顶点而不能执行规则1时，那么从队列头取一个顶点，并使其成为当前顶点。
如果因为队列为空而不能执行规则2，则搜索结束。

{
  create a queue Q //创建一个队列
  enqueue s onto Q //顶点s进队
  mark s as visited //
   while Q is not empty
   { 
      dequeue a vertex from Q into v    //将Q中顶点v弹出
      for each w adjacent to v          //v的每个邻接点w
       { 
        if w unvisited                  //w未访问过
         { 
          mark w as visited             //标记w已范围
          enqueue w onto Q              //w入栈
          } 
       } 
  }
}

实战

有 N 个房间，开始时你位于 0 号房间。每个房间有不同的号码：0，1，2，…，N-1，并且房间里可能有一些钥匙能使你进入下一个房间。

在形式上，对于每个房间 i 都有一个钥匙列表 rooms[i]，每个钥匙 rooms[i][j] 由 [0,1，…，N-1] 中的一个整数表示，其中 N = rooms.length。钥匙 rooms[i][j] = v 可以打开编号为 v 的房间。

最初，除 0 号房间外的其余所有房间都被锁住。

你可以自由地在房间之间来回走动。

如果能进入每个房间返回 true，否则返回 false。

示例 1：

输入: [[1],[2],[3],[]]
输出: true
解释:
我们从 0 号房间开始，拿到钥匙 1。
之后我们去 1 号房间，拿到钥匙 2。
然后我们去 2 号房间，拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间，我们返回 true。
示例 2：

输入：[[1,3],[3,0,1],[2],[0]]
输出：false
解释：我们不能进入 2 号房间。
提示：

1 <= rooms.length <= 1000
0 <= rooms[i].length <= 1000
所有房间中的钥匙数量总计不超过 3000。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/keys-and-rooms
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

DFS:

class Solution {
public:
    bool canVisitAllRooms(vector<vector<int>>& rooms) {
        _rooms = rooms;
        rooms_len = _rooms.size();
        int rooms_visited[rooms_len]={0};             //if the room was visited, set is to 1;
        unlocked.push_back(1);
        DFS(0,rooms_visited);                         //use DFS
        return rooms_len==unlocked.size();
    }
    void DFS(int index, int rooms_visited[]){
        rooms_visited[index] = 1;
        vector<int> it = _rooms[index];
        vector<int>::iterator sit;
        for(sit=(it).begin();sit!=(it).end();sit++){
            if(rooms_visited[*sit]!=1){
                unlocked.push_back(1);
                DFS(*sit,rooms_visited);              //search it
            }
        }
    }
private:
    vector<vector<int>> _rooms;
    vector<int> unlocked;
    int rooms_len;
};

BFS：

class Solution {
public:
    bool canVisitAllRooms(vector<vector<int>>& rooms) {
        queue<int> point;       //顶点队列
        point.push(0);          //初始点入队列
        int roo = 1;            //总room数量，需等于rooms.size()表示可全部访问
        int is_visited[rooms.size()] = {0};
        is_visited[point.front()] = 1;
        while(point.size()!=0){
            vector<int> new_room = rooms[point.front()];      //取出待搜新房间
            point.pop();                         //弹出队列第一个顶点
            vector<int>::iterator it;
            for(it=new_room.begin();it!=new_room.end();it++){
                if(is_visited[*it]!=1){                       //未搜
                    point.push(*it);                          //入队列等待搜取
                    is_visited[*it] = 1;
                    roo++;                                    //开的房间加1
                }
            }
        }
        return roo == rooms.size();
    }
};